Лидеры категории
 Лена-пена
Лена-пена
 М.И.
М.И.
 Y.Nine
Y.Nine



 •••
•••
Искусственный Интеллект
Искусственный Интеллект
Искусственный Интеллект
Как получили данную формулу
vvv
(750),
закрыт
3 года назад
Как из первой формулы получили вторую? Пожалуйста объясните все подробно




Лучший ответ
Сергей Фетисов
(680)
3 года назад
Подозреваю, что согласно приведённому свойству логистической функции:


vvvПрофи (750)
3 года назад
Это то понятно, а как из первой формулы получили вторую? Вот главная загадка для меня
Сергей ФетисовПрофи (680)
3 года назад
Так путём дифференцирования.
Далее по пунктам комментирую 4 строки вывода.
1. Начальное выражение
2. Ищем производную по w. Константный множитель слева остался.
3. Пользуемся свойством производной логистической функции, не забывая, что у нас не сигма (x) а сигма (f(x)). То есть домножаем справа ещё на производную аргумента.
4. Раскрываем производную суммы. То есть производная (w1 o1 + w2 o2 + .) по wj равна oj.
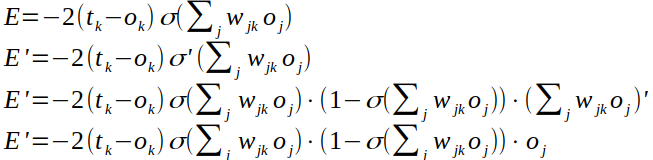
Далее по пунктам комментирую 4 строки вывода.
1. Начальное выражение
2. Ищем производную по w. Константный множитель слева остался.
3. Пользуемся свойством производной логистической функции, не забывая, что у нас не сигма (x) а сигма (f(x)). То есть домножаем справа ещё на производную аргумента.
4. Раскрываем производную суммы. То есть производная (w1 o1 + w2 o2 + .) по wj равна oj.
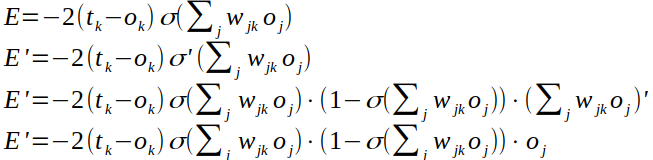
Остальные ответы
user49912
(51202)
3 года назад
А можно хотя бы пояснить, что скрывается за буквами и какая конкретно функция в данном контексте называется сигмоидой?
Пока это выглядит как обыкновенное взятие производной.
Пока это выглядит как обыкновенное взятие производной.
vvvПрофи (750)
3 года назад
сигмоида это y = 1\(1 + е^-x)
А без объяснения значений букв никак? Просто это будет очень долго
А без объяснения значений букв никак? Просто это будет очень долго
user49912
Оракул
(51202)
без объяснения я уже сказал: обыкновенное взятие производной
стандартные математические правила дифференцирования плюс какие-то сокращения и упрощения, основанные на знании того, что буквы из себя представляют
не можешь догадаться до упрощений сам - придётся объяснить буковки
Похожие вопросы
