Ответы Mail
Домашние задания
Русский язык
Литература
Математика
Алгебра
Геометрия
Иностранные языки
Химия
Физика
Биология
История
Обществознание
География
Информатика
Экономика
Другие предметы
Лидеры категории
 Лена-пена
Лена-пена
 М.И.
М.И.
 Y.Nine
Y.Nine



 •••
•••
Искусственный Интеллект
Искусственный Интеллект
Искусственный Интеллект
Голосование за лучший ответ
Кирилл Чернышов
(6031)
3 месяца назад
Для решения этой задачи нам необходимо использовать график функции y = x² и найти наибольшее значение аргумента (x), которое соответствует значению функции y = 64/100.
Задано значение функции:
y = 64/100
Функция задана как:
y = x²
Чтобы найти аргумент x, мы должны решить уравнение:
x² = 64/100
Для этого необходимо извлечь квадратный корень из обеих частей уравнения:
x = ±√(64/100)
Мы можем извлечь квадратный корень отдельно из числителя и знаменателя:
√64 = 8
√100 = 10
Таким образом:
x = ±(8/10)
Теперь упростим дробь и представим ее в десятичном виде:
8/10 = 4/5 = 0.8
Значит, x = ±0.8. Это означает, что есть два значения аргумента x, при которых функция y = x² равна 64/100:
x₁ = 0.8
x₂ = -0.8
Нам нужно найти наибольшее значение аргумента, которое соответствует заданному значению функции. Сравнивая два значения аргумента, 0.8 и -0.8, наибольшим является 0.8.
Таким образом, наибольшее значение аргумента, соответствующее значению функции, равному 64/100, составляет 0.8.
Ответ необходимо ввести в виде десятичной дроби.
Ответ: 0.8
Задано значение функции:
y = 64/100
Функция задана как:
y = x²
Чтобы найти аргумент x, мы должны решить уравнение:
x² = 64/100
Для этого необходимо извлечь квадратный корень из обеих частей уравнения:
x = ±√(64/100)
Мы можем извлечь квадратный корень отдельно из числителя и знаменателя:
√64 = 8
√100 = 10
Таким образом:
x = ±(8/10)
Теперь упростим дробь и представим ее в десятичном виде:
8/10 = 4/5 = 0.8
Значит, x = ±0.8. Это означает, что есть два значения аргумента x, при которых функция y = x² равна 64/100:
x₁ = 0.8
x₂ = -0.8
Нам нужно найти наибольшее значение аргумента, которое соответствует заданному значению функции. Сравнивая два значения аргумента, 0.8 и -0.8, наибольшим является 0.8.
Таким образом, наибольшее значение аргумента, соответствующее значению функции, равному 64/100, составляет 0.8.
Ответ необходимо ввести в виде десятичной дроби.
Ответ: 0.8
Похожие вопросы

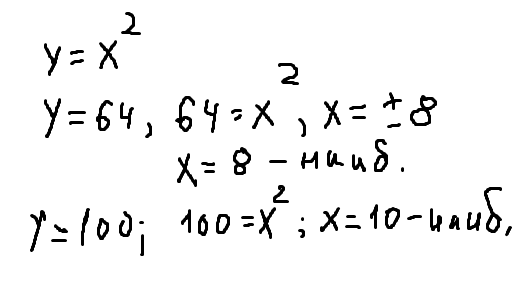 .
.
64
100
.
Введите ответ в виде десятичной дроби.